割り算の余りの性質 証明 357764-割り算の余りの性質 ��明

数学小話 中学校では教えてくれない数の性質 互いに素と余りの関係 日比谷高校のススメ

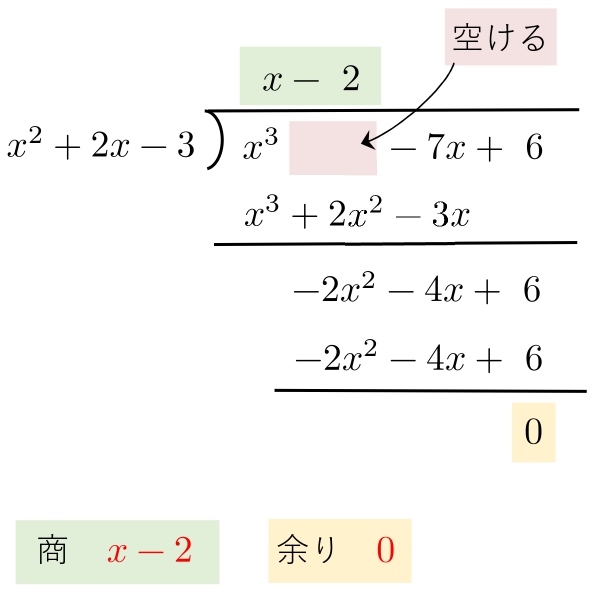
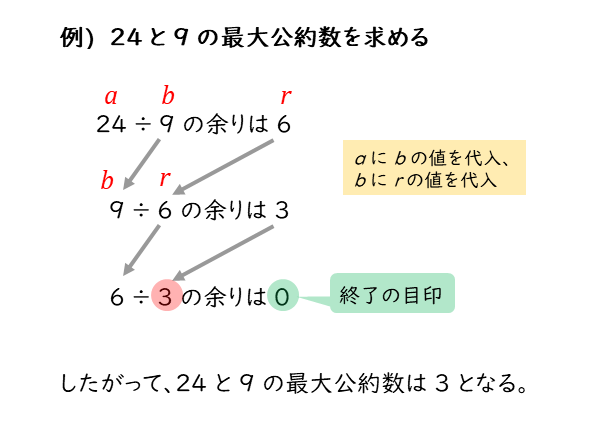
まとめ 整式を割った余りを求める問題は次のことがポイントとなります。 整式を1次式xαで割った余りはxαが0になる値x=αを代入して求める(剰余の定理)。 整式を2次以上の式で割った余りは，(余りの次数)＜(割る式の次数)となるように余りをおいて，割り算について成り立つ等式をつくって 整数nについて、\(n ^{2}\)を5で割った時の余りが全て 0、1、4のいずれかである事を証明せよ。 解答解説 nは無数にあるので、全てのn ^2を5で割って確認することはできません。 この様な時に剰余類の考え方が役に立ちます。

割り算の余りの性質 証明

割り算の余りの性質 証明-MathAquarium例題整数の性質 6 7 整数の分類の利用 n は整数とする。n2 を3 で割ったときの余りは0 か1 であることを証明せよ。 一般に，m を2 以上の自然数として，整数をm で割ったときの余りで分類すると，すべての整数は次の いずれかの形で表される。 割り算の基本 割り算は「 除法 」とも言い、 割り算の結果を 「 商 」と呼びます。 「 除 」には「 取り除く 」という意味があり、「 割り算 」とは「 いくつ取り除けるか 」という事です。 「 商 」は、むかし 商人 たちが「 自分たちの分け前や取り分を、はかる時 」に使っていたという説も

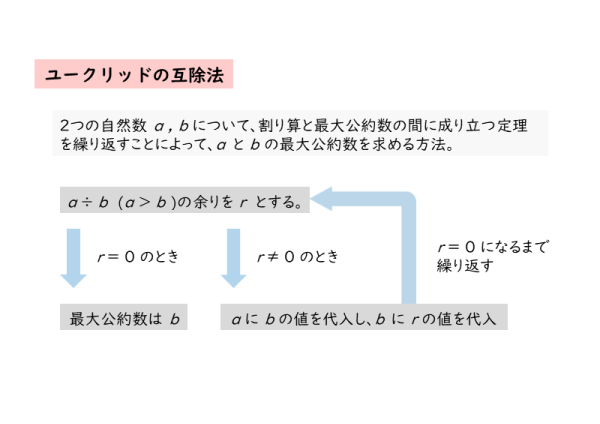
整数の性質 ユークリッドの互除法について 日々是鍛錬 ひびこれたんれん

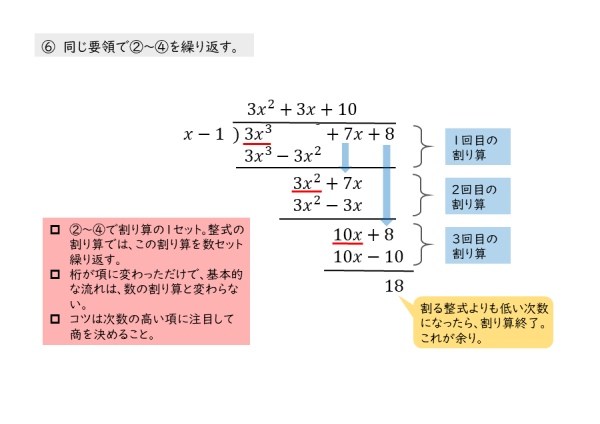
合同式の性質とその証明 合同式には、重要な性質（計算規則）があります。 \(1\) つ \(1\) つの性質とその証明を確認していきましょう。 合同式の和・差・積 複数の合同式において、 法が同じであれば 辺々を足し算・引き算・かけ算できます。 合同式を使って余りを求めるその2 例題2 2100 2 100 を 17 17 で割ったときの余りを求めなさい。 応用合同式 の最後で見た内容とほぼ同じです。 17 17 を法としたときに、 1 1 や −1 − 1 と合同となるような 2k 2 k を探すようにします。 計算していくと 式と証明｜割り算と整式の決定について その2（恒等式） 今回は割り算と整式の決定について学習しましょう。 すでに割り算と整式の決定について学習済みですが、ここでは恒等式の考え方を用いて整式を決定しようと言う内容です。 整式の割り算では

2数の和差積と余り：数A 準備整数の文字での表し方 数A倍数や余りの証明 数A余りによる整数の分類 数A連続する整数の積と証明 割り算と規則性の問題 LINE@始めました。 友達追加をよろしくお願い申し上げます。 勉強のやり方の相談・問題の解説随時募集しています！ お気軽にLINEしてください。 問題12 1,a,3,b 1, a, 3, b が繰り返し並んでいる。 ただし、 a,b a, b は定数とする。 （11 aをbで割ったときの商qと余りrを使って等式a=bqrの形が作れる 2 a=bqr (0≦r＜b)が成り立っているとき，aをbで割ったときの商がq，余りがrとなる （割られる数）=（割る数）×（商）（余り）となることを簡単な例で説明してみます．たとえば，26を7で割っ

割り算の余りの性質 証明のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

2	2	2
2	2	2
2	2	2
2	2	2
2	2	2
2	2	2
2	2	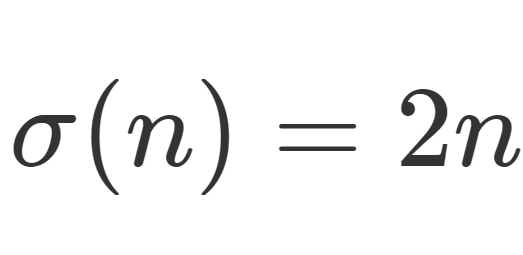2
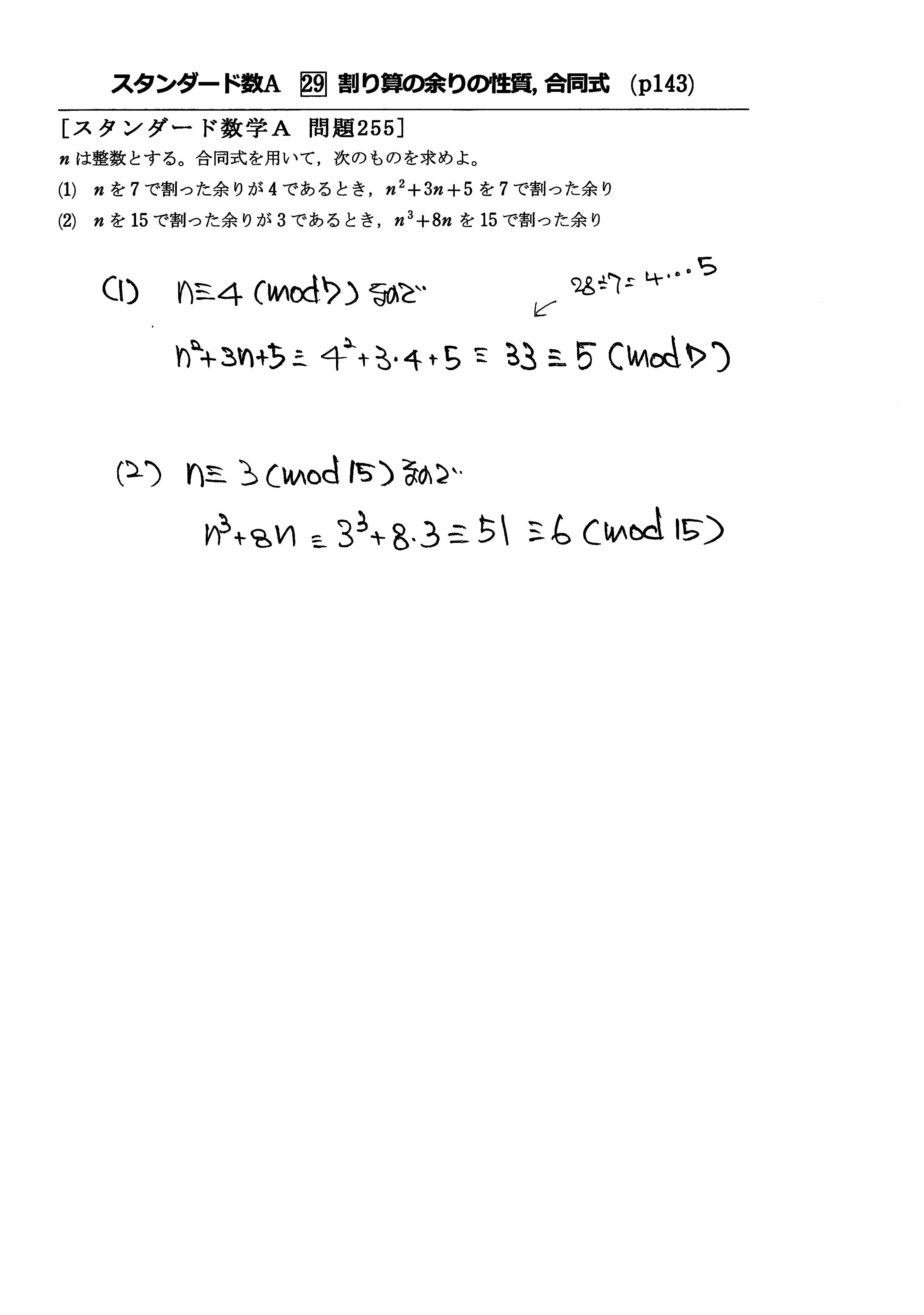2	2	2
2	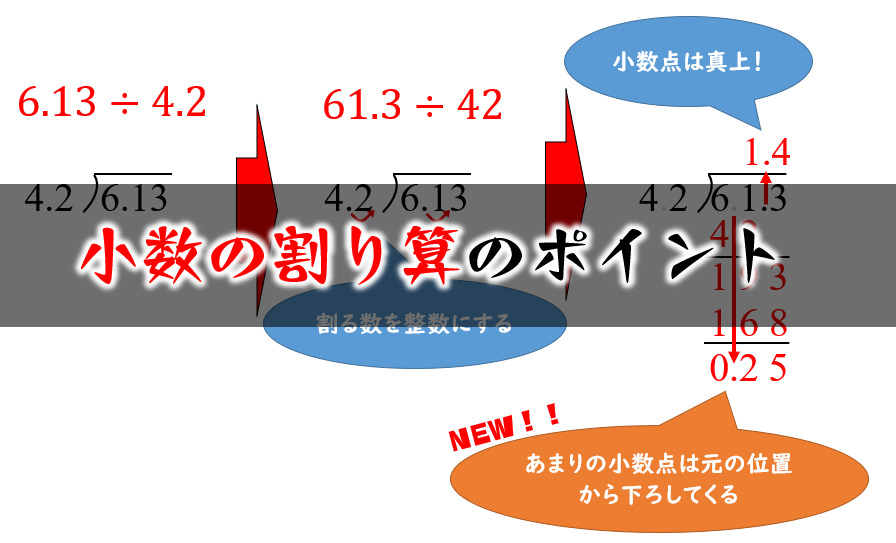2	2
2	2	2
2	2	2
2	2	2
2	2	2
2	2	2
2	2	2
2	2	2
2	2	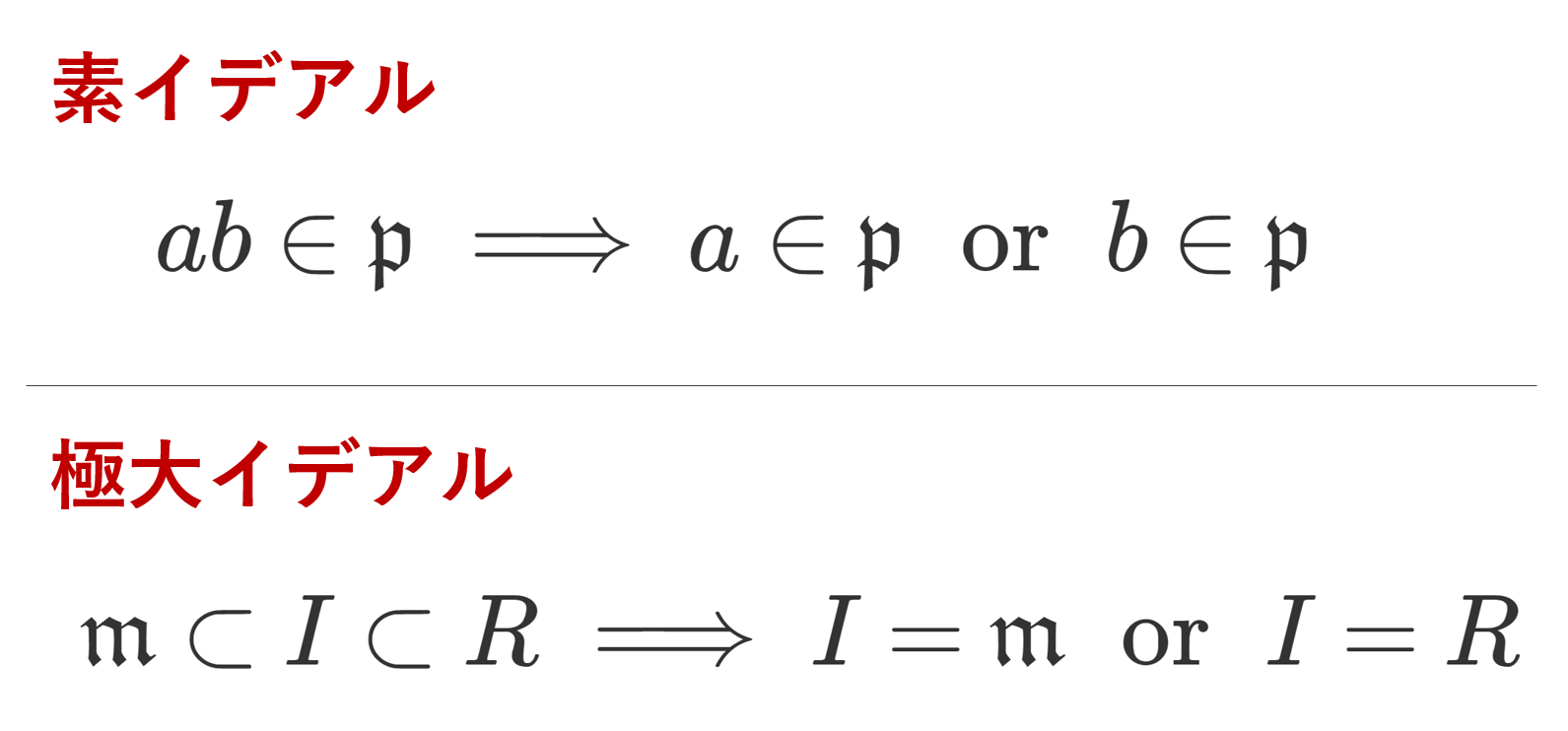2
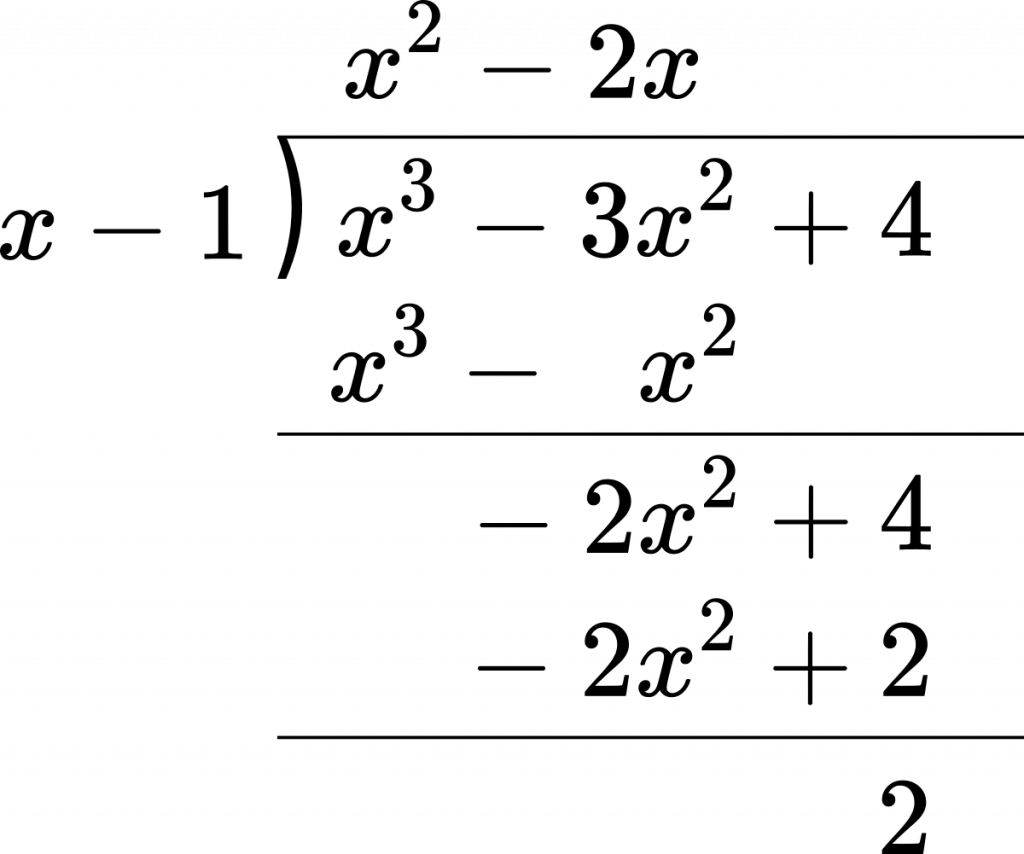2	2	2
2	2	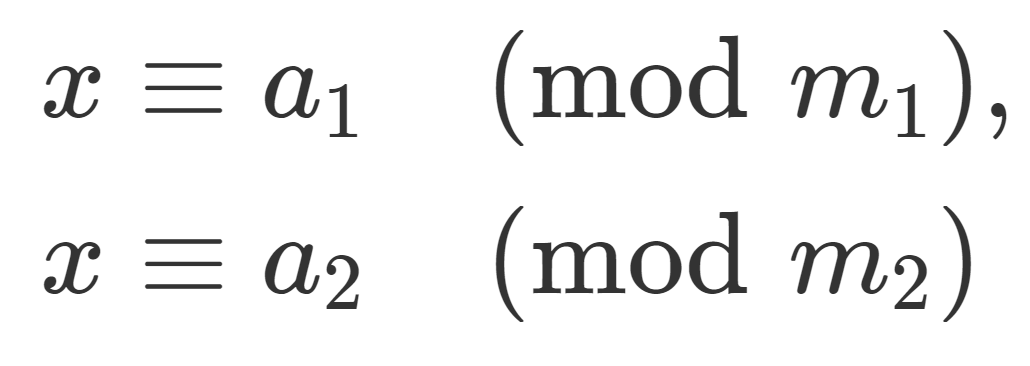2
2	2	2
2	2	2
2	2	2
2	2	2
2	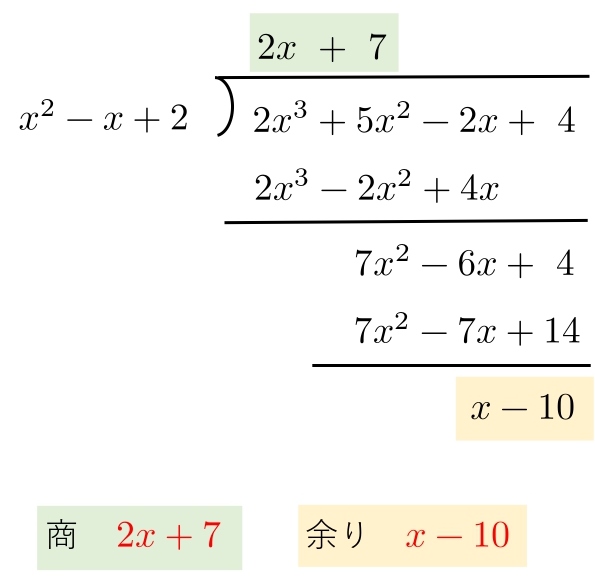2	2
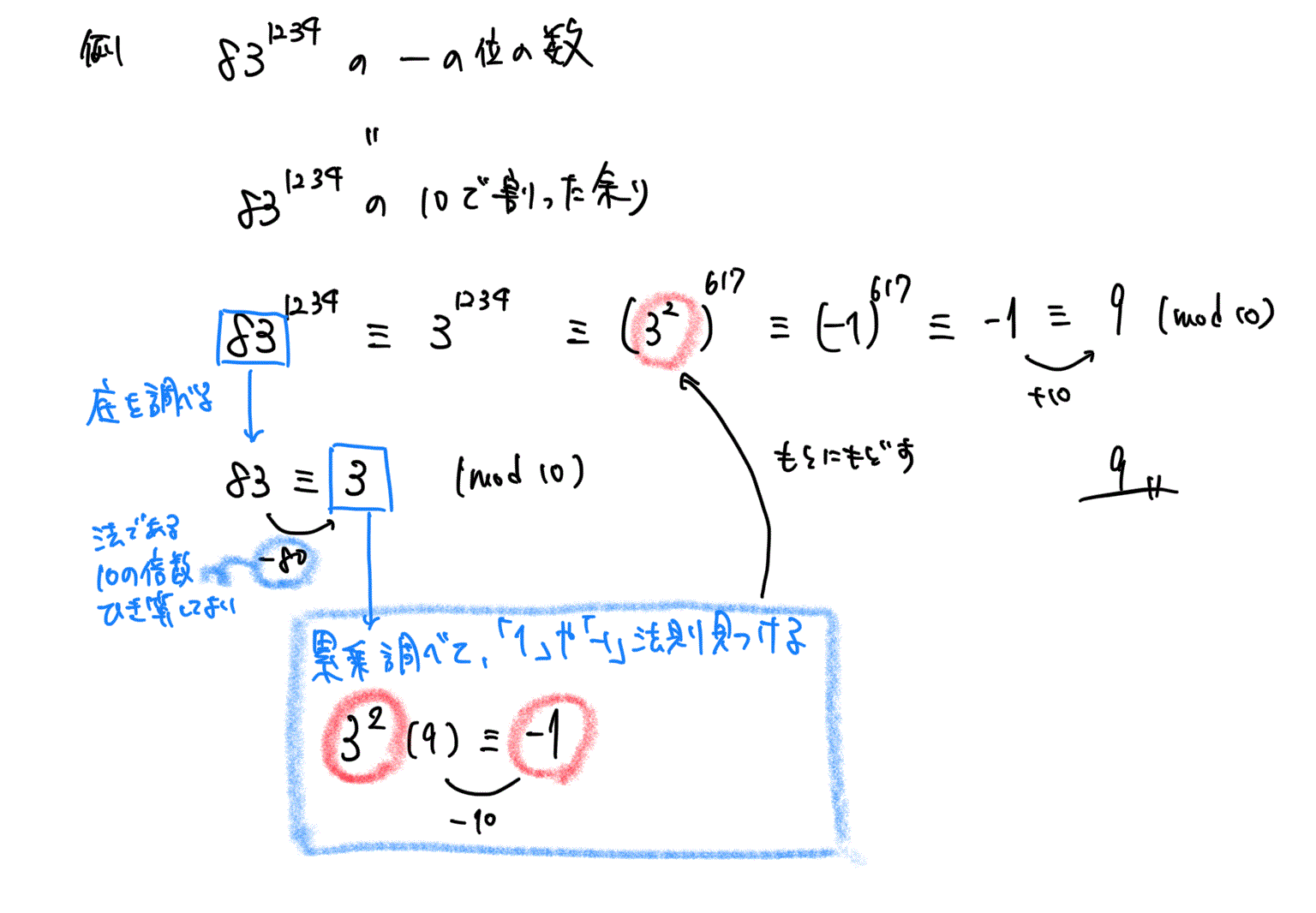2	2	2
2	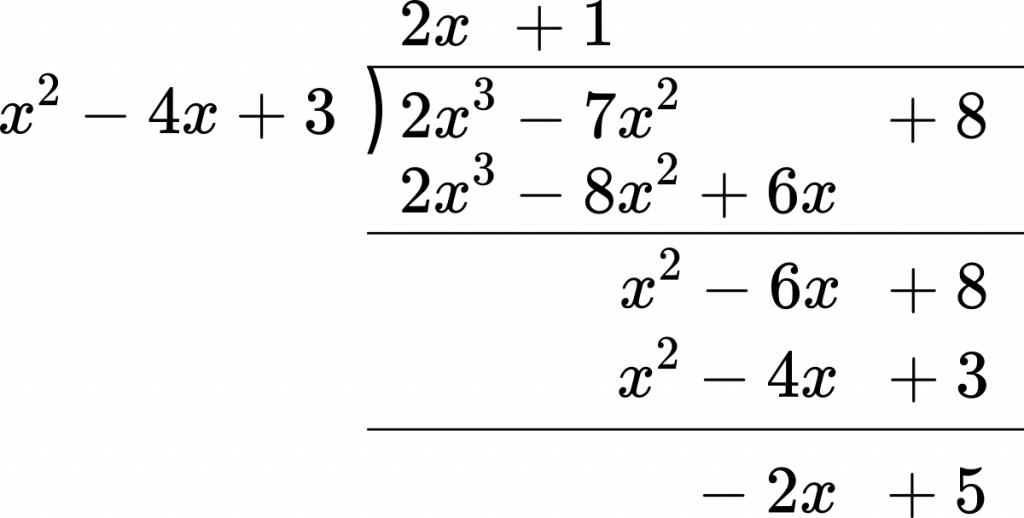2	2
2	2	2
2	2	2
2	2	2
2	2	2
2	2	2
2	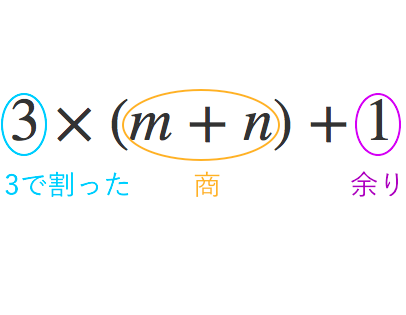2	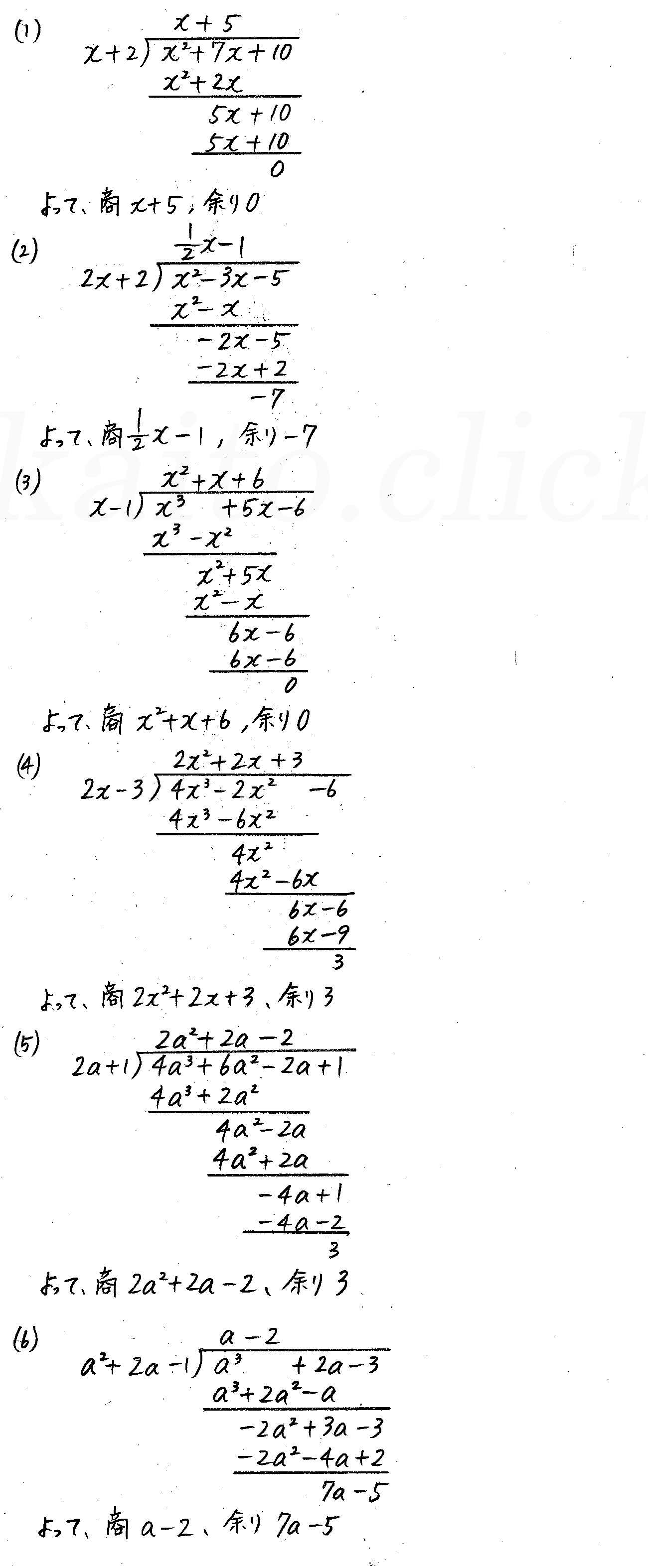2
2	2	2
2	2	2

 3024方べきの定理と2つの円の関係 (1) 303整数の性質 (40) 3031約数・倍数・整数の割り算と余り・合同式 (32) 3032ユークリッド互除法と不定方程式・N進法 (8) 4数Ⅱ (102) 401式と証明 (9) 4011整式の除法・分数式・二項定理 (6) 整数の性質 整数 基本整数の除法と商と余り 18年7月27日 ここでは、整数の除法（割り算）を行ったときの、商と余りについて見ていきます。 余りの範囲を制限すれば、商と余りの組は1組にできるので、よくやる方法としては、次のように定め

Incoming Term: 割り算の余りの性質 証明,