画像 分数 グラフ 座標 252410-分数 グラフ 座標

分数関数のグラフのかき方 高校数学 定期テスト対策 ベネッセ教育情報サイト

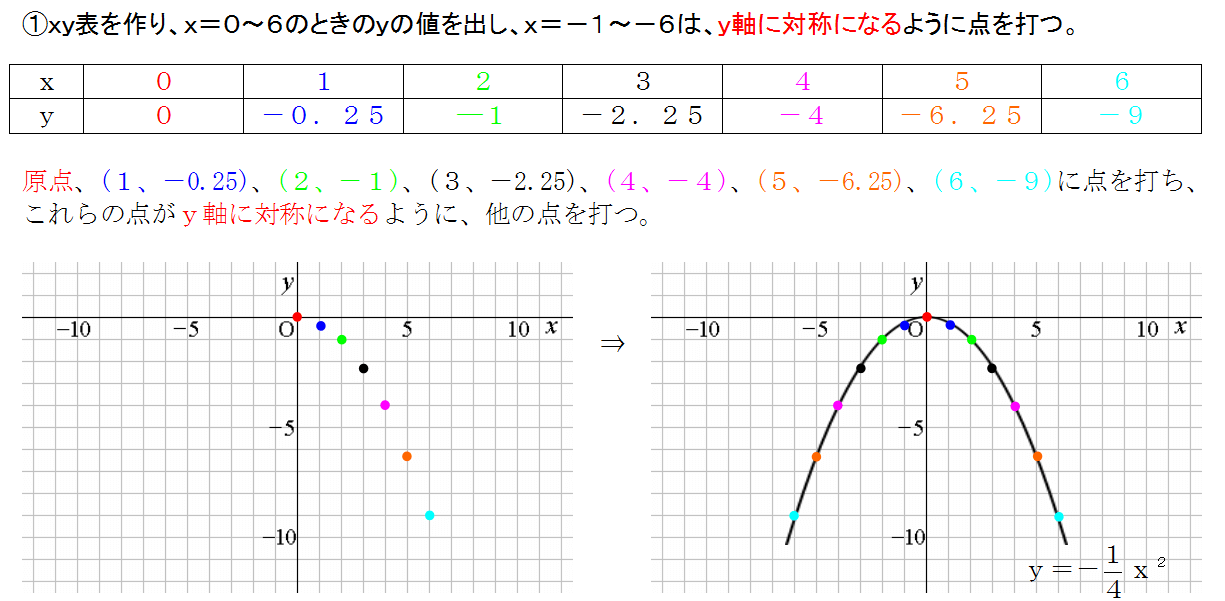
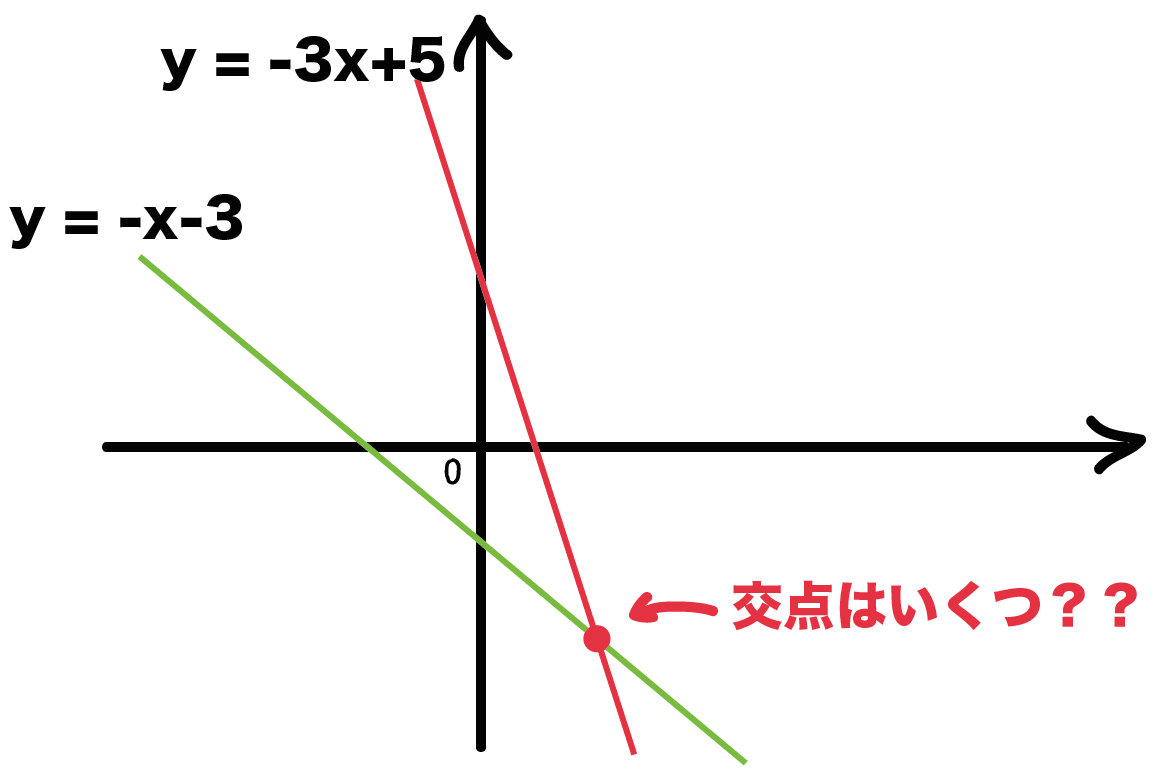
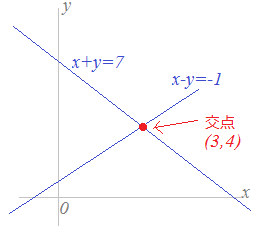
 グラフ関連の問題はどう解けばいいのか。 その辺りを詳しく説明していきます。 二次関数のグラフとはどういうものか 一次関数のグラフは、座標平面で直線でしたね。 二次関数のグラフの形状は「放物線」といい、次のような見た目です：一次関数 交点の座標の求め方\(1\) 交点の座標は次の方法で求められます。 \(1\)、一次関数の式を連立方程式として解く。 \(2\)、グラフを書いて交点の座標を調べる。 大切なのは 連立方程式の答えが交点座標になる。 という点です。

分数 グラフ 座標

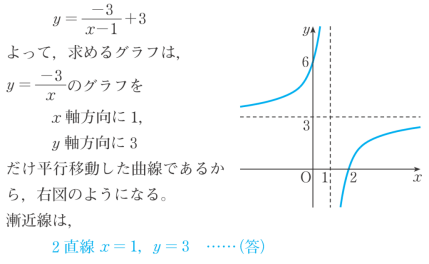
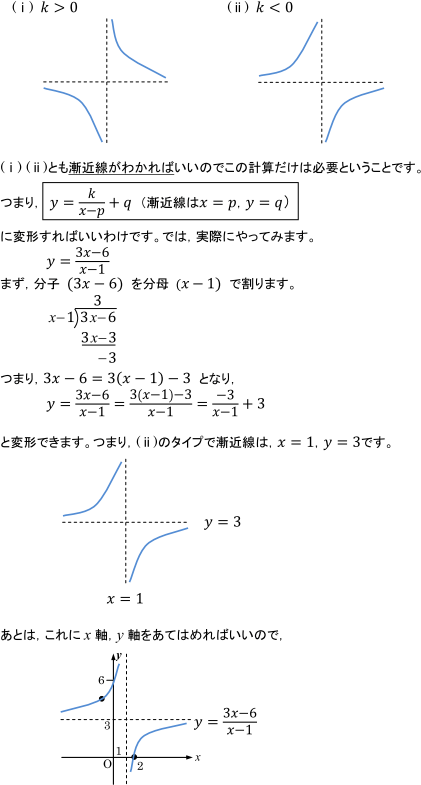
分数 グラフ 座標- 一次分数関数のグラフの漸近線 漸近線とはグラフが近づいていく直線（または曲線）のことです。 厳密には極限を用いて定義されますが，一次分数関数に関しては漸近線は極限の議論をしなくても分かります。 さきほどかいた二つのグラフを見れば★無料の中学メルマガ講座★毎週、問題と動画講義をお届け！ 勉強の習慣が身につく わかることが増えて楽しい 誰でも自由に学べる今すぐ無料

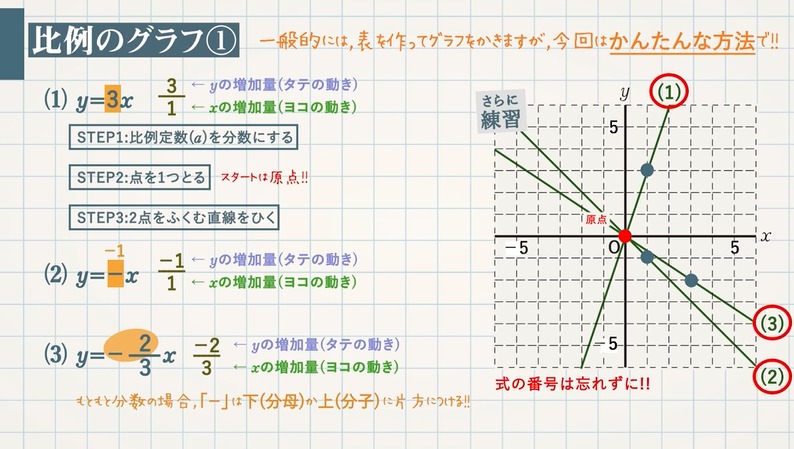
中1 比例のグラフのかき方 分数 日本語版 Youtube

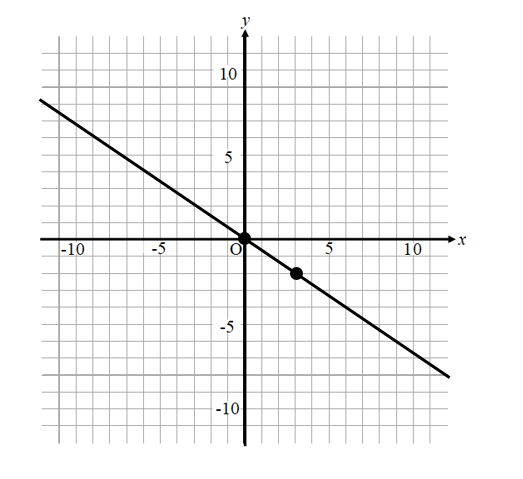
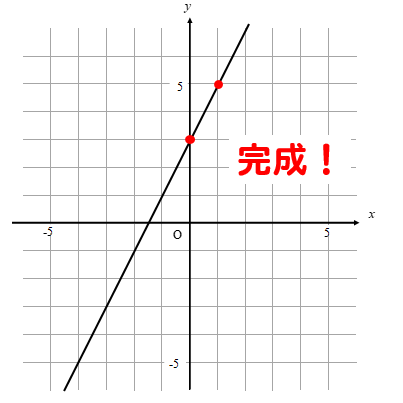
次のグラフに対応する比例の式を求めて，下の選択肢から1つクリックしてください． なお，赤丸で示した点は x 座標も y 座標も整数になっています． (1) 解説 やり直す 原点以外 で直線が通っている点を1つ見つけると， (1, 3) すなわち x=1 ， y=3 だからに断りがない場合，分数関数の定義域は，分母を にする の値を除く実数全体である。 分数関数のグラフと性質 1 分数関数 \ n s t のグラフは， \ n のグラフを 軸方向に s，\ 軸方向に t だけ平行移動した直角双曲線で， 漸近線は 直線 s，\ t である。 グラフのオプション "plot"でグラフを書く際に，いくつかのオプションがあります． プロットする点を増やす方法 plot (座標) によるグラフの描画は，区間を等間隔に区切ってできる25個の点をプロットし，それらを線分で結んで描いています．

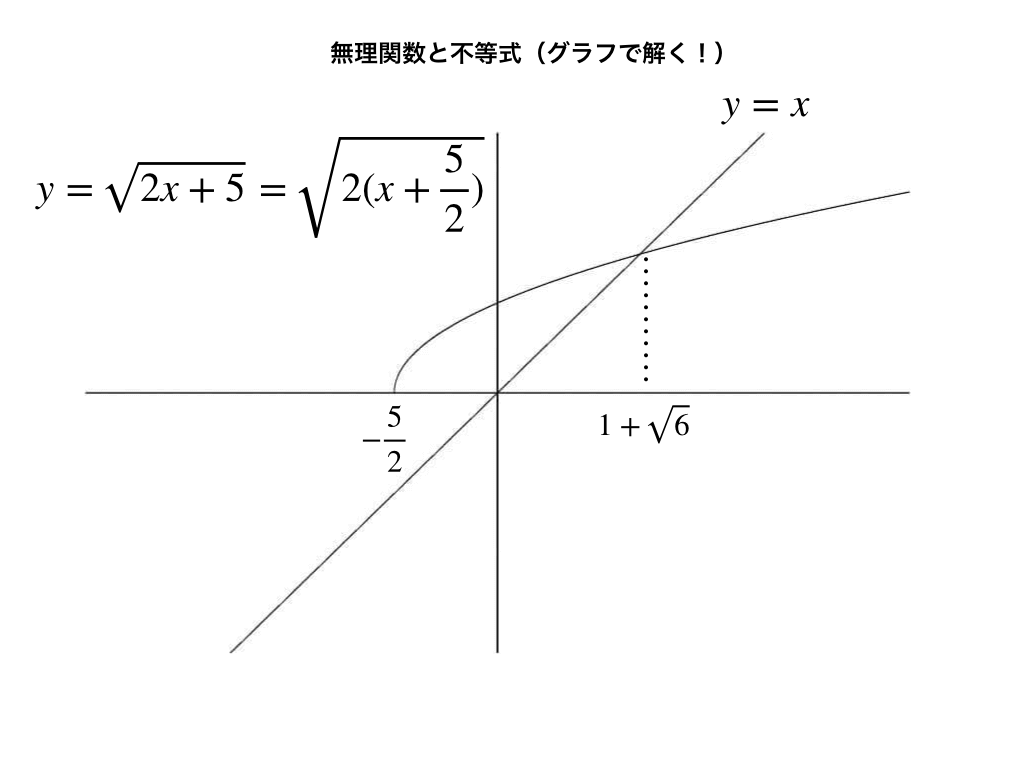
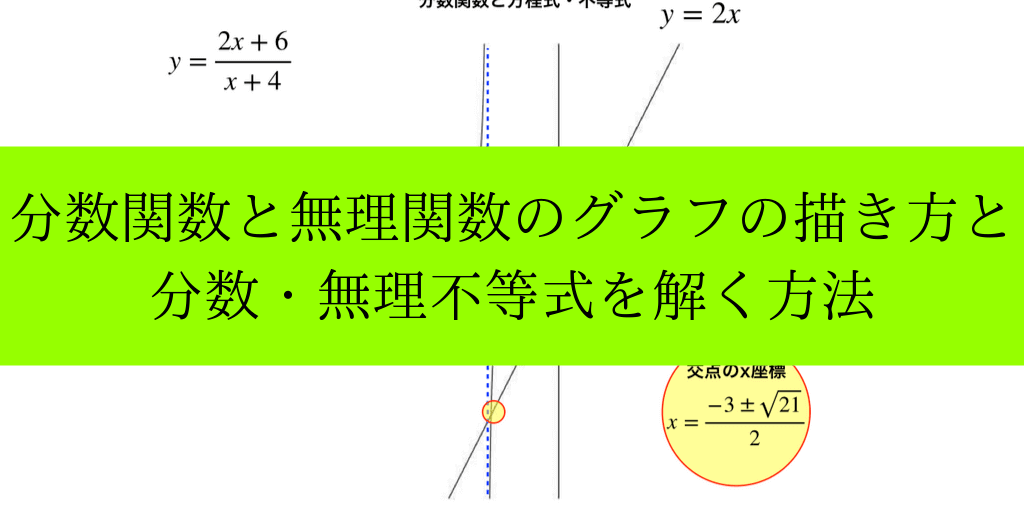
1次関数のグラフとは？5分でわかる描き方、特徴、式、傾き、分数との関係 切片と傾きの違い 切片と傾きの違いを下記に示します。 切片 ⇒ y=axbのbの値。1次関数の直線とy軸の交点の値。切片の座標は必ずx＝0となる 傾き ⇒ y=axbのaの値。 パターン3 「切片」と「座標」がわかっている場合 つぎは「切片」と「座標」がわかっている問題だね。 たとえば、つぎみたいなヤツさ↓↓ 例題 yはxの一次関数で、そのグラフが点（2, 11）を通り、切片3の直線であるとき、この一次関数の式を求めなさい。 グラフの書き方、分数不等式、微分積分を解説 22年3月16日 この記事では、「分数関数」についてわかりやすく解説していきます。 分数関数のグラフの書き方や不等式の解き方、微分積分のやり方なども説明しますので、この記事を通してぜひマスターし

分数 グラフ 座標のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

1	1	1
1	1	1
1	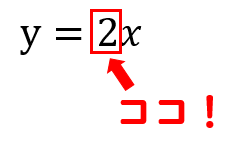1	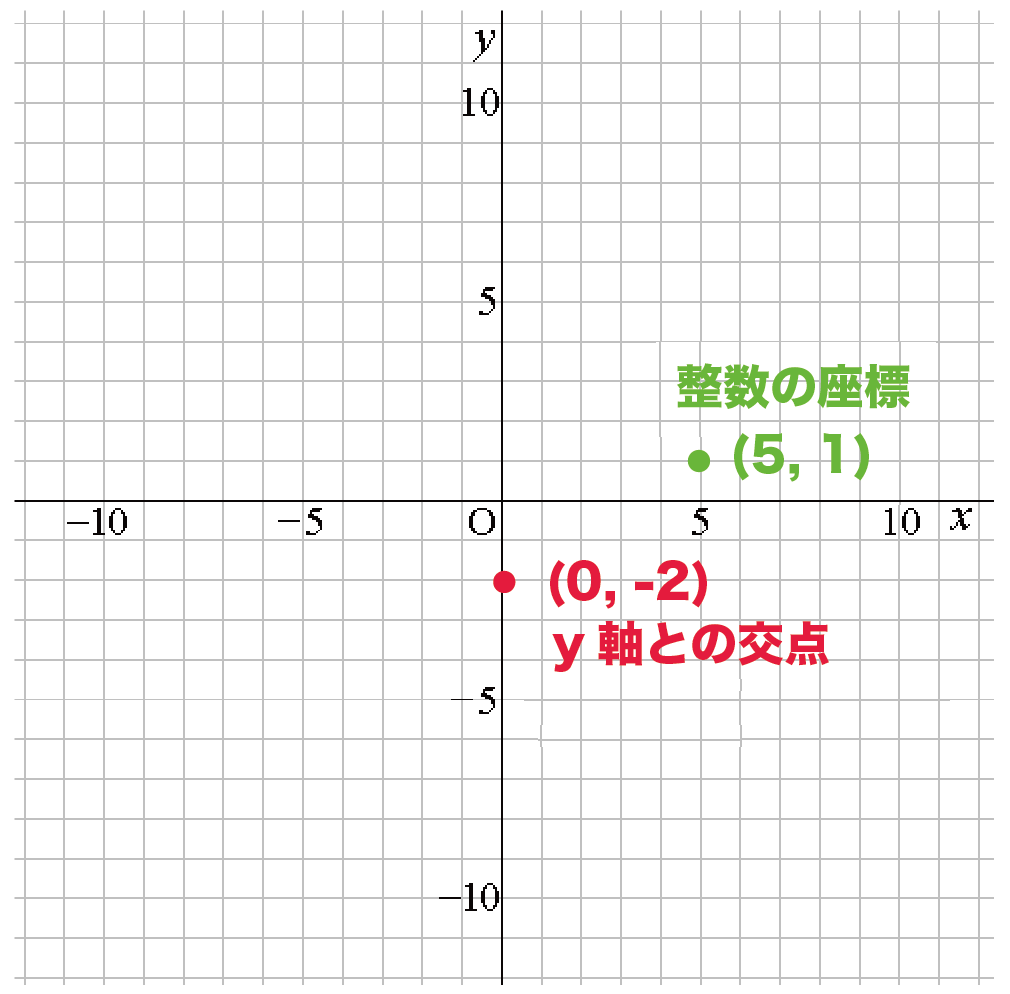1
1	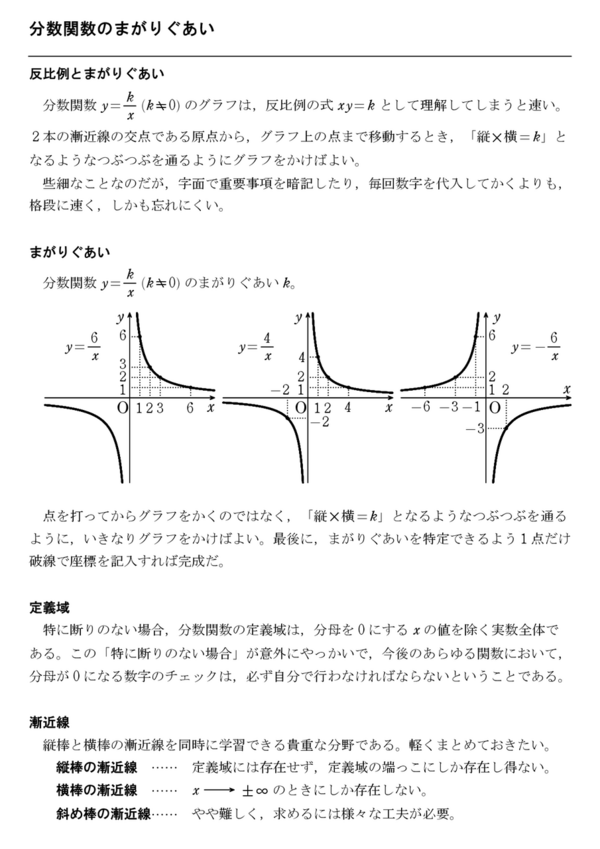1	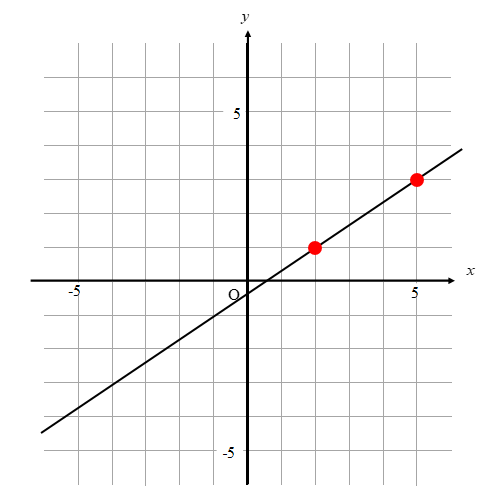1
1	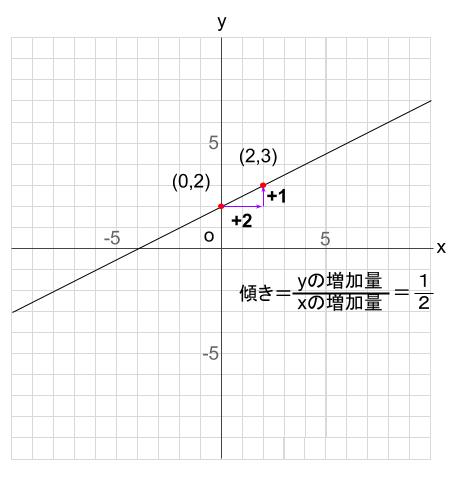1	1
1	1	1
1	1	1
1	1	1
1	1	1
1	1	1
1	1	1
1	1	1
1	1	1
1	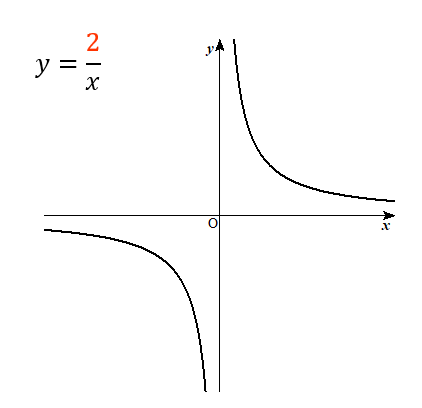1	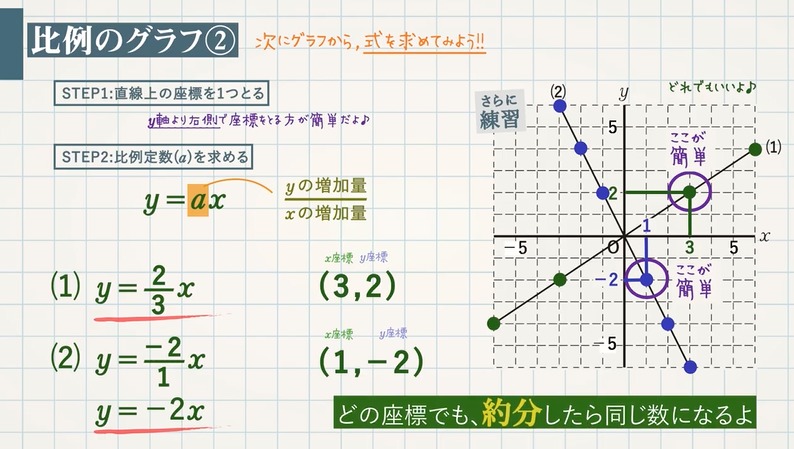1
1	1	1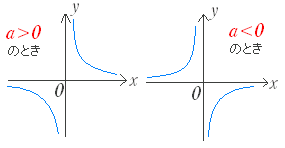
1	1	1
1	1	1
1	1	1
1	1	1
1	1	1
1	1	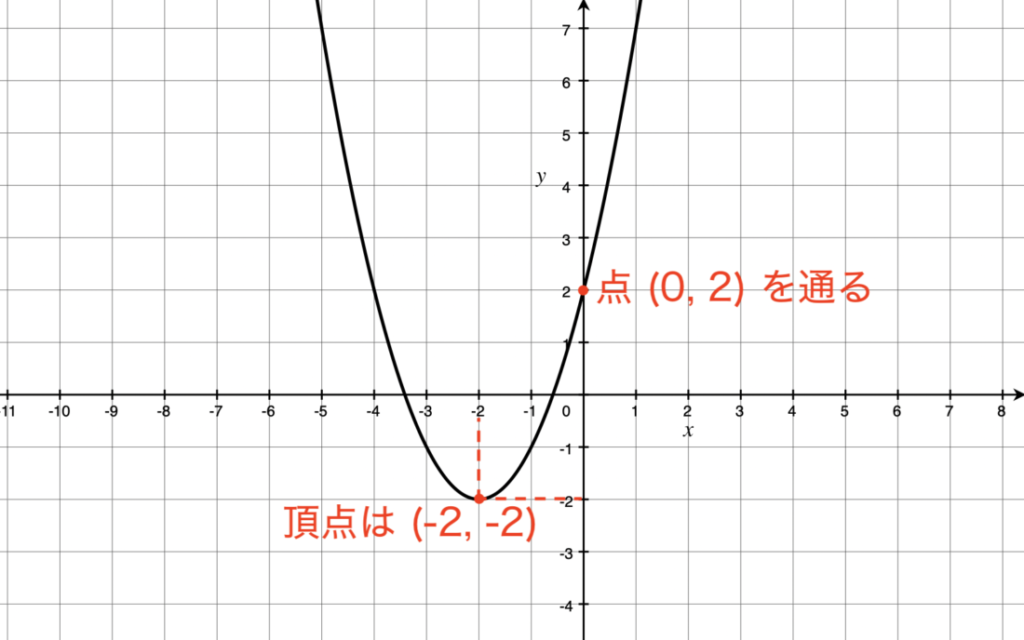1
1	1	1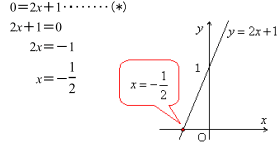
1	1	1
1	1	1
1	1	1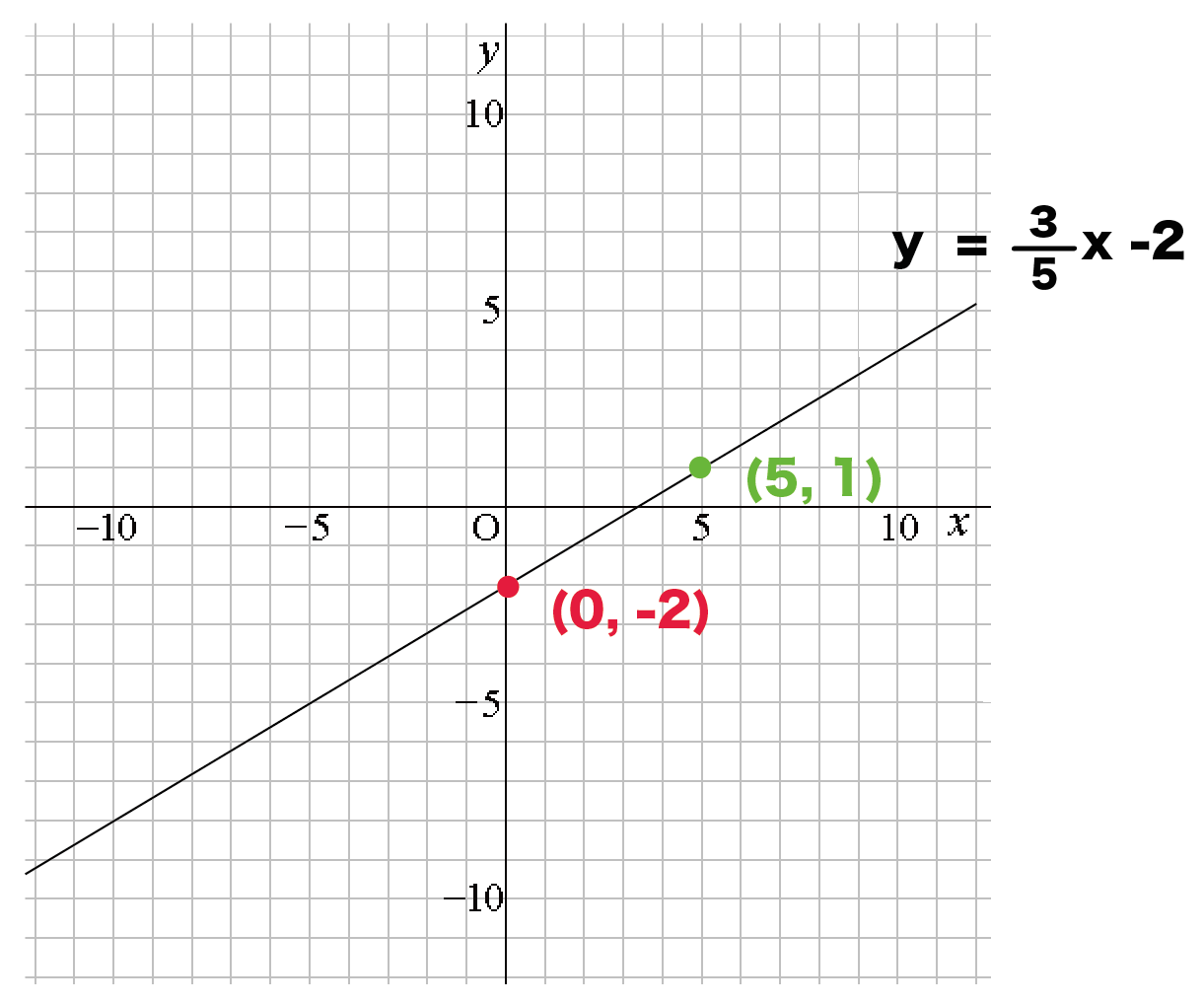
1	1	1
1	1	1
1	1	1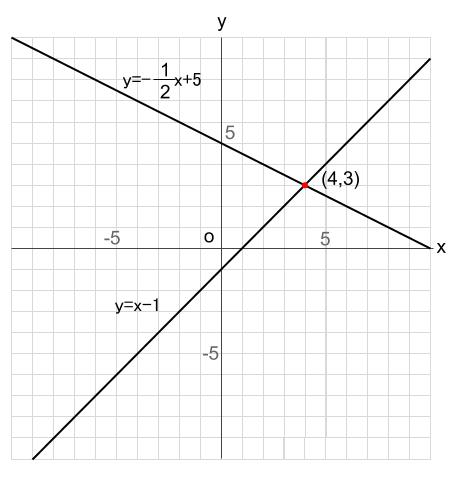
1	1	1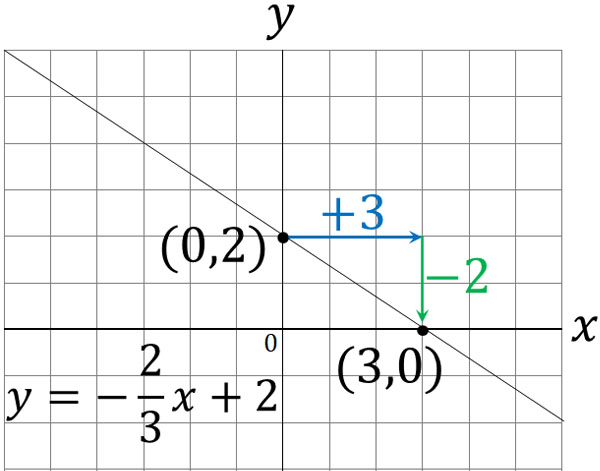
1	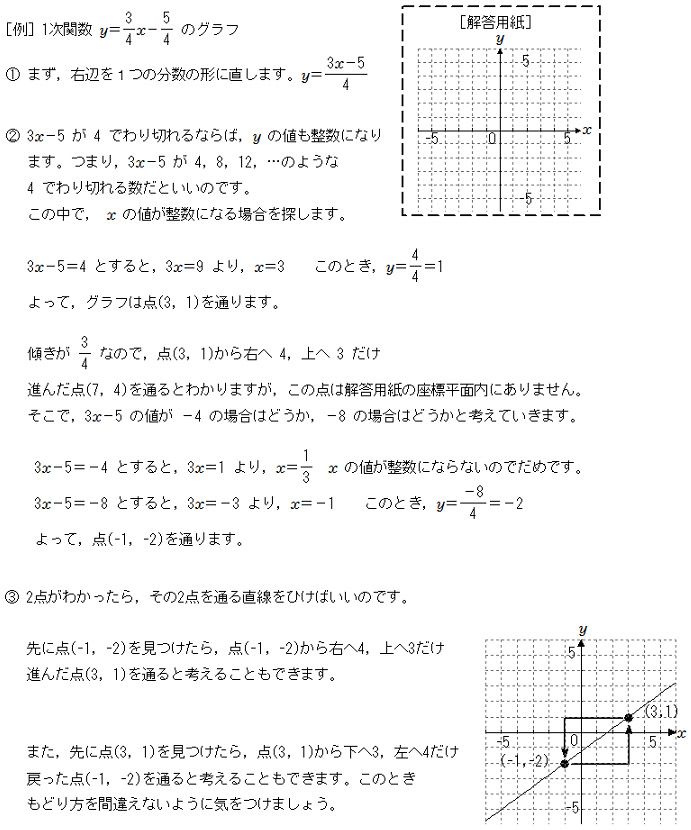1	1
1	1	1
1	1	1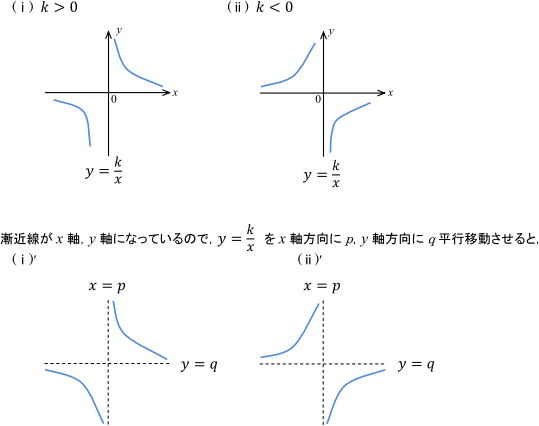
1	1	1
1	1	1
1	1

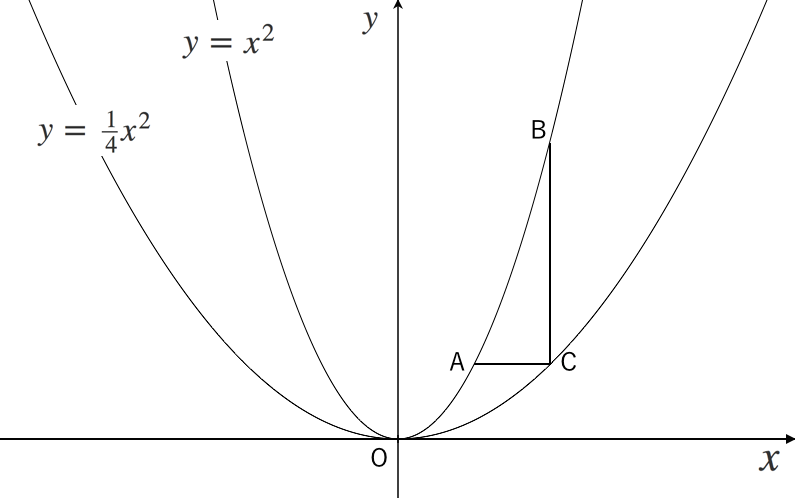
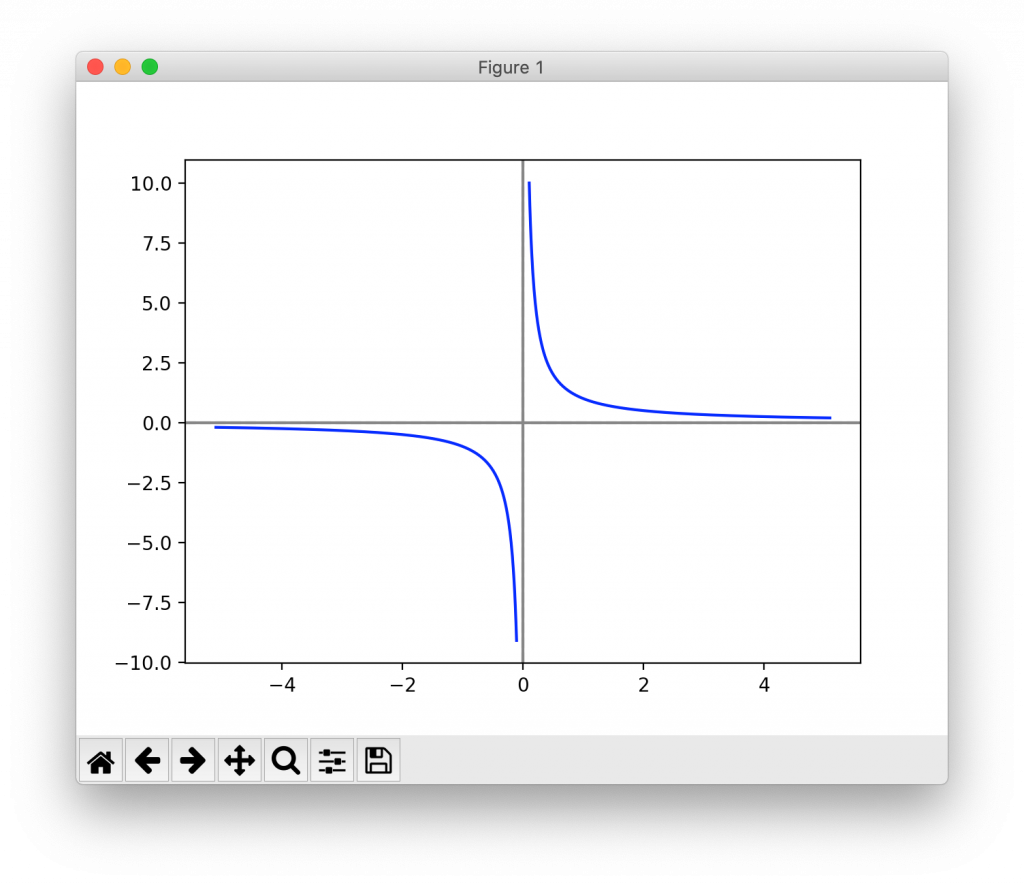
 こうした一次分数関数の式の中で、一番シンプルなものは、 a = 0 a = 0, d = 0 d = 0 とした場合でしょう。 k = b c k = b c とおけば、 y = k x y = k x となります。 これは、すでに見たことがある式です。 反比例ですね。 グラフは、次のように双曲線になります 中学数学 高校入試 二次関数 グラフ 分数を含んだ直線の出し方がわかりません！今まで分数含んでないパターンは2次方程式で解いてたんですけど、分数だとどうやってとけばいいのかわかりません！お願いします！ ！(この図は簡単に書いただけです)

Incoming Term: 分数 グラフ 座標,